Hugo Durney Wasaff1
RESUMEN
Gran parte de los nuevos estándares para sistemas de comunicación digital, concebidos para superar la creciente demanda por mayores velocidades de transmisión y niveles de eficiencia espectral, consideran el uso de modulaciones de amplitud no constante tales como M-QAM en formatos de OFDM. Una de las limitaciones más críticas para el funcionamiento de estos sistemas es la distorsión no lineal típicamente introducida por los amplificadores de alta potencia presentes en la cadena de transmisión. Este artículo resume la propuesta de un algoritmo de procesado de señal para la estimación adaptativa de la característica inversa de ganancia compleja de un amplificador no lineal en un esquema de pre/post- distorsión. Algunos resultados de simulaciones son presentados a fin de evaluar la efectividad del proceso de linealización propuesto y considerar posibles líneas futuras de investigación.
Palabras clave: Predistorsión, amplificadores, procesado de señal, sistemas no lineales, OFDM.
ABSTRACT
Many of the new digital communication standards, conceived to overcome the ever greater demands on bit rate capacity and spectral efficiency, consider the use of non-constant amplitude modulations such as M-QAM in OFDM formats. One of the major limitations on the performance of such systems is the non linear distortion typically introduced by high power amplifiers (HPA) in the transmission chain. This paper summarizes the proposal of a new signal processing algorithm for the adaptive estimation of the complex gain characteristic of a nonlinear HPA, in a pre/post-distortion scheme. Some simulation results are presented in order to evaluate the effectiveness of this linearization procedure and future related research to consider.
INTRODUCCIÓN
En los ultimos años la constante aparicion de aplicaciones multimedia y servicios integrados en sistemas de transmisión digital han dado lugar a una creciente demanda de capacidad de canal para la transmisión de datos. La coexistencia simultánea de usuarios con alta velocidad y eficiencia espectral (incluso en redes de frecuencia única) ha sido posible desde la implementación de tecnologías de acceso codificado, las que hoy representan un bajo costo gracias a la evolución de las capacidades del hardware de procesamiento digital de señales (DSP). En este contexto, el crecimiento de las comunicaciones a través de plataformas de banda ancha por vía alámbrica e inalámbrica ha hecho extensivo el uso de modulaciones de amplitud no constante. Tal es el caso de la integracion de formatos M - Q A M en sistemas multiportadora OFDM (Orthogonal Frequency Division Multiplexing). Dichos esquemas de transmisión, debido a su alta eficiencia espectral y robustez ante canales selectivos en frecuencia, ya han sido adoptados en el marco del desarrollo de diversos estandares internacionales. De hecho, actualmente se encuentra ya operativo un buen número de prototipos y sistemas OFDM para DAB (Digital Audio Broadcasting [1]) y DVB-T (Terrestrial Digital Video Broadcasting [2]), con un avance tecnológico que amenaza con un cada vez mas cercano " apagon" de los servicios de broadcasting analógico (analog switch-off) para dar paso a la radio y TV digital, hecho que en algunas zonas de Europa ya está siendo previsto aproximadamente para el año 2012. Otro ejemplo es la adopción de este formato en las nuevas redes inalámbricas de área local, personal y metropolitana a través de especificaciones tales como las IEEE 802.11/15/16 para W-LAN/PAN/ MAN y el estándar HIPERLAN II de la ETSI.
No obstante lo anterior, y en contraste a sus amplias ventajas, diversos estudios demuestran que los sistemas basados en OFDM presentan una altísima vulnerabilidad ante pérdidas de sincronismo y, en especial, ante la presencia de la distorsión no lineal típicamente introducida por los amplificadores de R.F. en el proceso de transmisión. Esto es debido a que la señal OFDM está caracterizada por una gran variabilidad en su envolvente, lo cual es comúnmente expresado como un alto nivel de PAPR (Peak-to-Average Power Ratio), parámetro que relaciona los valores máximo y promedio de la señal temporal. A consecuencia de esto, problemas como la interferencia por canal adyacente e intersimbólica afectan de manera crítica las prestaciones de estos sistemas. Por otra parte, la solución trivial de utilizar solo parte del margen dinámico amplificadores (back-off), a fin de evitar zonas de distorsion y saturación resultan especialmente inapropiada en el campo de las comunicaciones móviles, satelitales y, particularmente, en las nuevas aero- plataformas de radiocomunicación HAPS, donde la eficiencia de potencia en transmisión es primordial para lograr la máxima autonomía del equipamiento y de la nave de soporte.
Con todo lo expuesto, el comportamiento no lineal de los amplificadores de alta potencia o HPAs (High Power Amplifiers), constituye uno de los principales obstáculos para el funcionamiento de los sistemas de comunicación digital basados en OFDM. Afortunadamente, este nocivo efecto puede ser compensado mediante diversas técnicas clásicas de linealización cuyas variantes 'ad hoc' han sido propuestas e investigadas durante años. Entre dichas técnicas, la predistorsión digital ofrece óptimas condiciones para el diseño de linealizadores adaptativos, ya que puede ser fácilmente implementada sobre la información discreta de las señales de banda base. El objetivo general que se persigue es alcanzar el nivel de linealidad necesario para explotar al máximo las capacidades inherentes a cada modulación y, al mismo tiempo, alcanzar un máximo aprovechamiento de la potencia disponible. En el presente trabajo2, efectuamos una breve revisión de un modelo de distorsión no lineal típico, para luego presentar un sumario del diseño y evaluación de un esquema de pre/postdistorsión basado en un algoritmo iterativo que considera, como principal aporte, la optimización bidimensional de un reducido número de coeficientes de interpolación que identifican adaptativamente la característica inversa de ganancia compleja de un HPA, tanto en función de la particular morfología no lineal de dicha curva como también de la distribución de probabilidad de la señal muestreada.
Fig. 1 Linealización mediante (a) predistorsión y (b)postdistorsión.
MODELO DE DISTORSIÓN NO LINEAL
Los HPAs introducen dos tipos de distorsión no lineal, AM/AM y AM/PM, sobre la amplitud y fase de la señal transmitida respectivamente. En las condiciones de ancho de banda de las señales comúnmente utilizadas en sistemas OFDM, ambos tipos de distorsión pueden ser caracterizados ya sea como funciones de transferencia o ganancia no lineal, sin memoria y dependientes de la amplitud de entrada al HPA. Si consideramos un modelo genérico de una señal banda base bx (t ) y, simplificando la notación, dejamos implícita la dependencia temporal,
la entrada al HPA estaría dada por:
donde ux = |bx| corresponde a la amplitud de la envolvente mientras x es la componente de fase instantánea de la señal. De este modo, la salida distorsionada del amplificador puede ser expresada como:
donde alternativamente se expresa la amplificación como la aplicación de funciones de transferencia no lineal independientes sobre la amplitud y fase, y luego como una ganancia multiplicativa compleja, también depen- diente del módulo de entrada, tal que A[u]=|bG[u]| representa la distorsión AM/AM, mientras se expresa la distorsión AM/PM como una componente no lineal aditiva sobre la fase original. Los dispositivos comerciales de amplificación de potencia en RF utilizan comúnmente dos tecnologías diferentes. Por una parte, están los HPA basados en tubos de ondas progresivas (TWTA) y, por otra, aquellos basados en dispositivos de estado sólido (SSPA). La ventaja principal de los últimos, en términos de comportamiento no lineal, es que introducen un nivel de distorsión AM/PM muy inferior. Sin embargo, aspectos como la respuesta de frecuencia y los retardos electrónicos (memoria) aun mantienen a los TWT (traveling-wave tubes) en una posición predominante en aplicaciones de alta frecuencia, especialmente en sistemas de microondas. Así, entre los modelos disponibles para caracterizar HPAs, optamos por el modelo de A.M. Saleh [3] para TWTA sin memoria. Este es de hecho el modelo más universalmente referido enla literatura, y normalmente es formulado a través de las siguientes expresiones:
Aquí, A[.] y Φ[.] corresponden a las características de transferencia no lineal AM/AM y AM/PM, respectivamente. A partir de estas relaciones, es posible definir un modelo equivalente de ganancia no lineal compleja el cual puede ser expresado de la siguientemanera:
A través de procedimientos algebraicos simples, es posible determinar las operaciones inversas teóricas correspondientes a las expresiones en (3) y (4). De este modo, tal como se ilustra en la figura 1, las características AM/AM y AM/PM inversas, denotadas A^-1 y Ψ respectivamente3, pueden ser aplicadas indistintamente como bloques de pre o postdistorsión (PD) para obtener, en ambos casos, una transferencia lineal normalizada ideal (ganancia unitaria) al menos dentro del margen dinámico previo a la saturación. La figura 2(a) muestra las características AM/AM y AM/PM del modelo expresado en las ecuaciones (3) para αa= 2 , βa= βΦ =1 y Φsat= π 3 de manera que tanto la amplitud de saturación de entrada como la de salida quedan normalizadas a la unidad. En la misma figura se representan las funciones de transferencia inversa teóricas de PD para estas curvas. Asimismo, en la figura 2(b) se representan las características teóricas AM/AM directa e inversa, pero esta vez definidas como ganancias multiplicativas dependientes de la amplitud de entrada a cada bloque. De (4) resulta evidente que | G PM [u x] | = 1 y, por tanto, este factor multiplicativo introduce la misma distorsión en fase que se obtiene con Φ[ux ]. Así, las curvas AM/PM de la figura 2(a) en conjunto con las curvas de ganancia AM/AM de la figura 2(b) expresan el modelo no lineal utilizado en nuestras simulaciones.En estas gráficas es importante observar que la ganancia de PD AM/AM tiende a presentar una pendiente infinita a medida que se acerca a la zona de saturación. Esto representa una limitación absoluta para cualquier sistema que intente interpolar dicha zona de la curva. Por otra parte también se observa que la curva de PD AM/PM no se obtiene simplemente al hacer −Φ[.] (intuición trivial asociada a una distorsión aditiva), sino que una compensación adecuada de esta distorsión mediante PD requerirá verificar
que es la expresión general para la función de PD AM/ PM que compensa perfectamente la distorsión no lineal de fase introducida por un HPA cuya característica AM/ AM tiene un inverso ideal A–1[]. De similar forma es posible encontrar que una ganancia ideal de pre/post distorsión debe satisfacer la siguiente equivalencia redundante: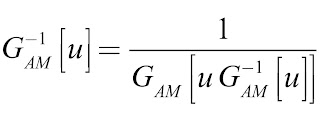
donde podemos observar que la estimación de G^-1AM^[.] no es tan directa como obtener simplemente el inverso multiplicativo de GAM [ .] , sino que implica la necesidad de una identificación de la función inversa, lo cual en definitiva corresponde a un problema de inversión de sistemas.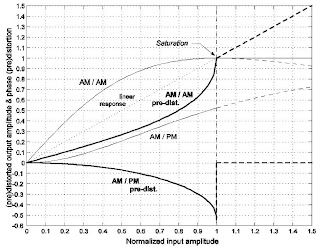
Fig. 2 (a) Características de transferencia AM/AM y AM/PM normalizadas del modelo de Saleh y sus respectivos inversos teóricos para pre/post- distorsión. (b) La misma característica no lineal AM/AM y su inversa teórica expresadas como ganancias multiplicativas.
FORMULACIÓN GENERAL DEL ALGORITMO
Si en los esquemas alternativos de la figura 1 denominamos Gˆ 1[.] a la estimación de la ganancia compleja asociada a los bloques de PD, podemos expresar la construcción de la señal de error de compensación para cada caso. Asumiendo implícita la dependencia respecto a la variable de tiempo discreto n, para una determinada frecuencia de muestreo, se obtienen las siguientes señales de error instantáneo (escalares):
Como es bien sabido, los algoritmos de optimización basados en métodos de gradiente descendente ejecutan una búsqueda de un mínimo para una función de coste normalmente basada en el error cuadrático medio (MSE). La dependencia de dicha función de coste respecto de los coeficientes a optimizar debe, idealmente, ser cuadrática a fin de asegurar la convergencia hacia un mínimo absoluto, evitando así el riesgo de hallar un mínimo local. Desde esta perspectiva, resulta claro que la señal de error en, asociada a una estructura de pre- distorsión, no está bien condicionada para este tipo de optimización iterativa, ya que una función de coste basada en |epre|^2 presentará dependencias de orden superior respecto de los coeficientes que describen el modelo no lineal G^-1[.], los cuales se hallan ya insertos en otra funcion no lineal G[.]. En cambio, la estructuradel error en (7) sí permite establecer una función de coste con dependencia cuadrática en los coeficientes que describen al PD. No obstante, se ha de tener en cuenta que la aplicación de la postcorrección estimada sobre las señales a la salida del HPA conllevaría evidentes desventajas a nivel de implementación al tener que trabajar con señales de alta potencia en RF. Esto nos permite concluir que:
1. La estructura de postdistorsión es adecuada para la etapa de entrenamiento adaptativo de coeficientes, pero resulta inconveniente para ejecutar la corrección misma en la señal.
2. La estructura de predistorsión ofrece facilidades para su implementación sobre las señales de baja potencia en banda base. Sin embargo, no es adecuada para la etapa de entrenamiento de los coeficientes de PD.
Por lo tanto, la estrategia final desarrollada contempla la estimación de los coeficientes que optimizan un bloque de postdistorsión para luego, en cada paso del algoritmo, ir volcando estos coeficientes hacia un bloque encargado de ejecutar la predistorsión sobre la señal de entrada. Este procedimiento está representado más adelante en la figura 4
Funciones de activación difusa
Para estimar y aproximar la curva de ganancia de PD y su posterior aplicación sobre las muestras de la señal procesada, se define un set de coeficientes de ganancia compleja α =[α0... αNC-1] que, asociados a funciones de activación por intervalos, interpolan linealmente el valor de ganancia asociado a una entrada determinada. En la figura 3 se definen en general dos tipos de funciones de interpolación donde el rango válido de entrada [o,Asat] del bloque de PD es dividido en NI intervalos, definidos a su vez por un conjunto de Nc=N1+1 puntos denominados "centroides" agrupados en el vector C=[C0 ...CN-1]. Así, para un valor 0≤u0 k con una entrada se cumple que:
Si consideramos que el sistema de la figura 4 opera con bloques de N muestras, podemos definir el error de adaptación del post distorsionador como la expresión vectorial (12).
Fig. 3 Funciones de activación difusa para interpolación lineal de la curva de predistorsión a través de los coeficientes de ganancia compleja α. (a) Triangulares (tipo 1), (b) y (c) de pendiente positiva y negativa (tipo 2).
Fig. 4 Estructura adaptativa del algoritmo de pre/ postdistorsión. Los coeficientes de ganancia compleja y la distribución de los centroides que definen las funciones de activación son adaptados de acuerdo a la minimización del error de postdistorsión. Luego, estos valores estimados son volcados hacia el predistorsionador para efectuar la corrección.
donde Dy es una matriz diagonal (NxN), cuya diagonal principal es By, Λ(NxNC) es la matriz de activación de los coeficientes, generada mediante las definiciones ee aplicadas para las amplitudes contenidas en |by|. Con esto, la minimización de | e |^2= e^H * e se formula como una típica optimización LMS para actualizar lo coeficientes de ganancia del PD. Esto se expresa para cada iteración como:
Donde "o" corresponde al producto vectorial elemento elemento y µα es la constante que define el paso de actualización.Estrategia de adaptación bidimensional
La búsqueda de los coeficientes α que aproximan con un mínimo error la función de PD puede ser efectuada a base de (13) con una distribución de centroide equiespaciados en [0, Asat]. Sin embargo, un patrón uniforme de funciones tipo 1 no toma en cuenta la distribución de probabilidad (PDF) del módulo de la señal de entrada al PD. A consecuencia de esto, habría una lenta o nula adaptación de aquellos coeficiente asociados a zonas de baja probabilidad de activación. La envolvente de una señal OFDM presenta una PDF Rayleigh con una muy baja probabilidad en zona cercanas a la saturación. En contraste, es precisamente en esta región donde la curva de PD presenta cambio más significativos y, por tanto, requiere de mayo resolución para interpolar la morfología no lineal. Este razonamiento explica la necesidad de plantear un algoritmo que optimice alternadamente tanto los coeficientes de ganancia en α como la distribución de centroides en c . Así, considerando una versión escala de (12), con
e = bx - by*λ^t*(uy*α, la función de coste basada en el MSE tiene una estructura con doble
dependencia.
donde σ^2x es la potencia promedio de bx(n) y los arreglos r= E*{bx*by*λ} y R=E{|by|^2*λ*λ^2} dan cuenta de la dependencia del error respecto a la distribución de centroides ya que éstos determinan el nivel de activación de los intervalos respecto a los valores esperados de by(n). La minimización de (14) en función de los coeficientes α ya fue establecida en (13). Para minimizar (14) respecto de c definimos la distancia entre centroides correlativos como un número positivo distinto de cero, esto es:
donde δk es una variable intermedia a través de la cual se adapta la distancia entre centroides y ∆min es una distancia mínima que evita el cruce o superposición de centroides.De este modo, si fijamos c0=0. Luego, fijando la posición del último centroide en cN=Asat el ancho de cada intervalo puede ser expresado como una proporción si se normaliza respecto a este rango máximo haciendo Pk= ∆k/Asat. Así, la posición de los centroides y la adaptación de c puede ser formulada en términos de estas proporciones. Al adaptar el valor proporcional de cada intervalo en lugar del ancho mismo, mantenemos el rango de entrada [0, Asat] inalterado pese a los cambios de posición de los centroides. Modificar un valor Pk implica una reducción o incremento distribuido a lo largo de todos los intervalos restantes cumpliendo con la restricción ∑Pt=1. Con todo esto, el gradiente que permite minimizar el error respecto de la distribución de centroides presenta la siguiente estructura final:
Ésta es una expresión escalar, para una iteración en que la amplitud de una muestra u activa el intervalo k. Este gradiente debe ser resuelto para todos los valores contenidos en el vector δ = [δ1... δN]. La resolución detallada de para la estimación del gradiente queda fuera del alcance de este sumario, sin embargo puede hallarse en el anexo 6.A de la referencia [4].Finalmente, la expresión que actualiza las variables que controlan la distribución adaptativa de los centroides queda:
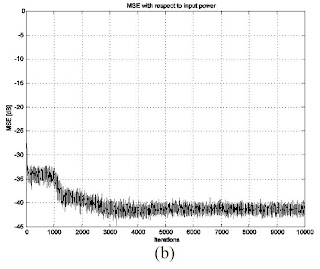
RESULTADOS Y CONCLUSIONESLa funcionalidad del algoritmo de PD presentado en este sumario fue exitosamente comprobada via simulación, implementando una cadena de transmisión OFDM que incluia un HPA no lineal basado en el modelo de Saleh. En esta sección extractamos sólo cuatro ejemplos. Las figuras 5(a) y 5(b) muestran la estimación de las curvas de ganancia inversa utilizando sólo 4 coeficientes entrenados, según el algoritmo de optimización bidimensional. Alli se utiliza una señal de prueba con PDF uniforme en amplitud y fase. En una primera etapa (primeras 1000 iteraciones) sólo se adapta el vector de ganancias hasta la convergencia a un óptimo, manteniendo fijos los centroides con distribución uniforme. Luego se les da la libertad de relocalizarse alternadamente, obteniendo una mejoria en el error de adaptación de aprox. 5dB. Las flechas indican el desplazamiento de los centroides desde sus posiciones originales hasta las optimizadas. Se observa como el algoritmo concentra los coeficientes de interpolación en la región de la curva cuya morfologia requiere mayor resolución. La figura 5(c) muestra, en términos de densidad espectral de potencia, los efectos de la compensación de la distorsión no lineal sobre una señal OFDM genérica de 52 subportadoras activas. El error residual de compensación (e0 en Fig.4) dentro y fuera de banda experimenta una mejoria de aproximadamente
3dB cuando la posición de 4 coeficientes de predis- torsión es mejorada respecto de una distribución inicial uniforme de centroides. Finalmente, en la figura 5(d) podemos observar el efecto de esta corrección respecto de la distorsión no lineal sobre una constelación de 2048 simbolos 16-QAM transmitidos sobre una de las
52 subportadoras. Los resultados obtenidos en diversas pruebas sugieren, como una interesante futura etapa de investigación, la implementación hardware del proceso completo de linealización, esta vez incorporando el efecto de memoria que presentará el sistema en tiempo real debido principalmente a la presencia de etapas de filtrado analógico.
Fig. 5 Estimación de las curvas de ganancia inversa.REFERENCIAS
[1] ETSI EN 300 401 V1.3.3. European Standard for Radio Broadcasting Systems. Digital Audio Broadcasting (DAB) to mobile, portable and fixed receivers. May 2001.
[2] ETSI EN 300 744 V1.4.1. European Standard for Digital Video Broadcasting (DVB). Framing structure, channel coding and modulation for digital terrestrial television. January 2001.
[3] A . A . S a l e h . " F r e q u e n c y - i n d e p e n d e n t a n d frequency-dependent nonlinear models of TWT amplifiers". IEEE Trans. on Comm. Vol. COM-29. Nº11, pp. 1715-1720. November 1981.
[4] H. Durney. "Adaptive pre-distortion for nonlinear high power amplifiers in OFDM systems". Tesis para optar al grado de doctor. Universitat Politècnica de Catalunya (UPC). July 2004.
Asignatura: CRF
Publicado: Dujeiny J Sánchez Q.
No hay comentarios:
Publicar un comentario